So, in the world of population genetics, as in the real world, people are often interested in diversity, and in how that diversity is distributed. In biological contexts, quantifying these things is important because it gives us insight into the processes – like reproduction, migration, selection, etc. – responsible for generating the observed patterns of diversity.

Here I look at how racial diversity is apportioned among counties (or county equivalents) in each of the 50 states, using two different statistics derived from the population genetics and ecology literature. Hit the jump for the analysis, and scroll down to skip the introduction and go straight to the maps.

One of the earliest and most enduring quantities in population genetics is F_ST. This quantity (along with various closely related “F”s with different subscripts) is an attempt to create a metric of population differentiation that is independent of the overall level of diversity. There are a variety of ways of formulating F_ST, depending on the type of data you’re thinking about, but all are something like this:

F_ST = (D_b – D_w) / D_b

Here, F_ST is a measure of differentiation between or among subpopulations. D_w is the diversity within subpopulations, and D_b is the diversity among subpopulations. As you can see, if you simply double the level of diversity (both within and among subpopulations), this measure of differentiation will be unchanged.

The concept of F_ST was developed 80-90 years ago, primarily by Sewall Wright, who examined and characterized some of its properties within highly simplified and idealized models of population structure. Then, 40-50 years ago, people started thinking about ways to estimate this quantity from genetic data. A lot of F_ST-related statistics have been developed, but I will described just one here, which compares the observed and expected levels of heterozygosity:

G_ST = 1 – H_O/H_E

H_E is the observed level of heterozygosity. Roughly speaking, we look at some gene all of the individuals in the population. Each person has two copies of the gene. If the two copies are the identical, the person is homozygous; if they are different, the person is heterozygous. The observed heterozygosity simply the fraction of people who carry two different copies.

The expected heterozygosity, H_E is calculated by taking all of the genes in the population and mixing them together. Now, draw two gene copies at random and ask, what is the probability that the two gene copies are different?

If the population is completely well mixed, H_O and H_E will be nearly the same, and G_ST will be close to zero. Elevated levels of G_ST result from non-random mating. For example, if the population consists of two isolated subpopulations, those subpopulations will tend to contain different versions of the gene, but there will be no one who has one copy of a variant from subpopulation 1 and a variant from subpopulation 2. Thus, there will be a reduced number of heterozygotes in the population, relative to what you would get if you mixed all of the genes in the two subpopulations together.

This notion of heterozygosity is not limited to genetic contexts, however, and we can do the equivalent calculation for any trait that can be divided into distinct categories (even if those categories are somewhat arbitrary social constructs like “race”).

Here’s an illustration. I have taken data from the 2009 American Community Survey, aggregated at the level of individual counties. I calculate the “observed heterozygosity” from the frequencies of different races in each county. Imagine that within each county, we paired people at random. The H_O calculated here is the fraction of these randomly paired couples who would have mixed-race children. In this calculation, I have assumed that if one parent self-identifies as “two or more races,” the children are mixed race, independent of the race of the other parent. Also, for simplicity, I have aggregated all subdivisions of “hispanic” into a single category. The H_E here is calculated from the same random-mating procedure applied at the level of the entire state.

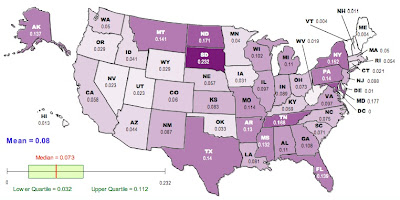
Here is a map of the results, generated using the free, online map generator from the National Council of Teachers of Mathematics:

Darker colors correspond to higher values of G_ST.

Now, it has been known for a long time that F_ST is not particularly well behaved. It is sensitive to things like the total number of distinct gene variants in the population and the total number of subpopulations. Recently, researchers have begun developing corrections to estimators of F_ST that are more robust to these deviations from the ideal models originally studied by Wright. One such correction was published a couple of years ago by Lou Jost, who proposed a metric, D, which demonstrably has many desirable properties that we would like to see from a statistic that describes population differentiation. In terms of the heterozygosities that go into G_ST, D is calculated like this:

D = [(H_E-H_O)/(1-H_O)][n/(n-1)]

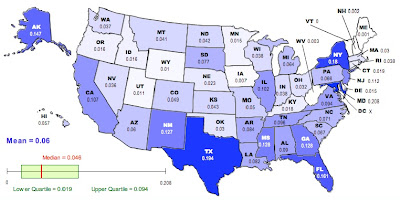
where n is the number of subpopulations. We can recalculate the racial “population differentiation” at the county level for each state. The new map looks like this:

As in the previous map, darker colors represent higher values of D.

Now, there are a lot of reasons to exercise caution in interpreting these values. The Jost correction used to generate the second corrects for certain problems associated with G_ST, but there is still an issue in that this analysis is based on aggregation at the county level. The geographical extent of counties varies enormously from state to state; the meaning of being in the same county in Utah is quite different from being in the same county in New York. Furthermore, the frequencies and identities of the groups vary among states in a way that will matter much more to any sociological analysis than will the numbers presented here. The F_ST-related statistics used here have been developed in the context of biological data, with the goal of understanding biological processes that are not necessarily analogous to the social processes that have driven the distribution of various groups in the US.

On the other hand, it is a lot more fun NOT to exercise caution. To that end, here is your list of the ten most racially differentiated states based on Jost’s D (second map):

Maryland, Texas, New York, Florida, Alaska, Mississippi, Georgia, New Mexico, New Jersey, California

And the ten least differentiated:

Vermont, Maine, New Hampshire, West Virginia, Iowa, Wyoming, Utah, Delaware, Minnesota, Idaho

If we go back to the raw G_ST (first map) the top-ten most differentiated are:

South Dakota, Maryland, North Dakota, Tennessee, New York, Montana, Texas, Pennsylvania, Florida, Alaska

And the least:

Vermont, Maine, Delaware, New Hampshire, Hawaii, West Virginia, Connecticut, Nevada, Utah, Oregon

I will leave irresponsible speculation and stereotyping of the residents of different states as an exercise for the reader.

JOST, L. (2008). GST and its relatives do not measure differentiation
Molecular Ecology, 17 (18), 4015-4026 DOI: 10.1111/j.1365-294X.2008.03887.x