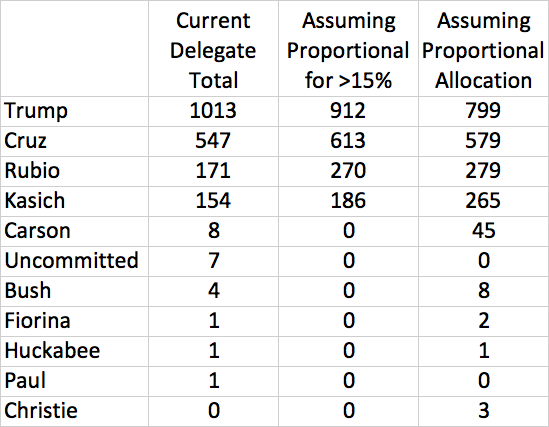
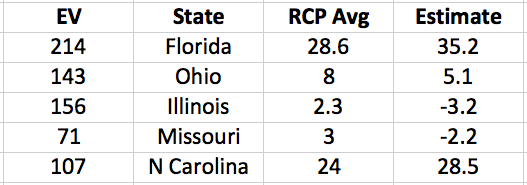
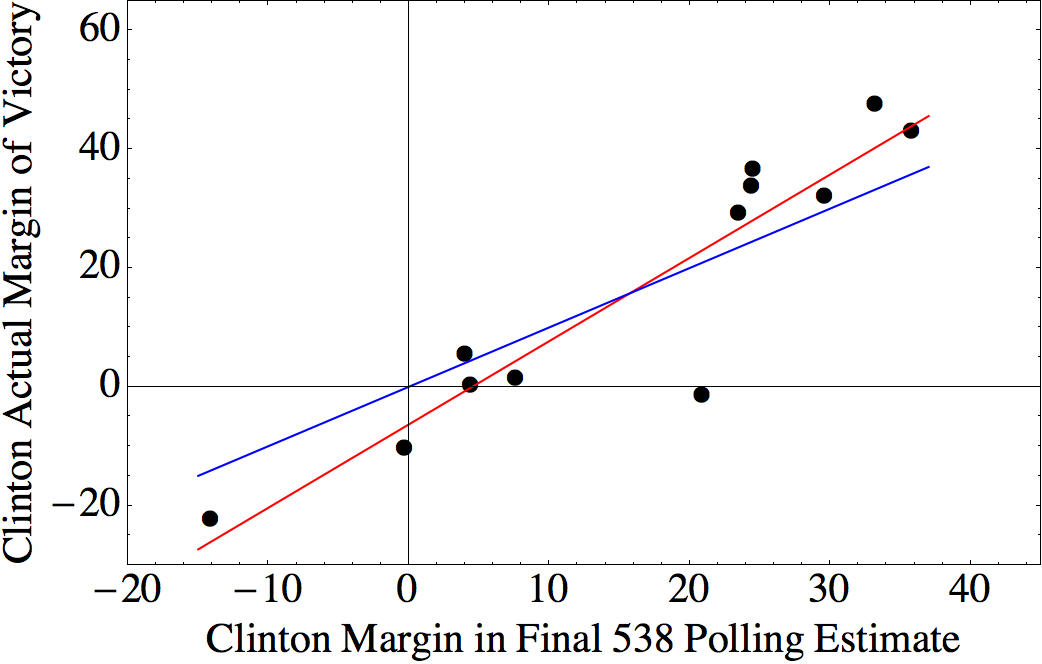
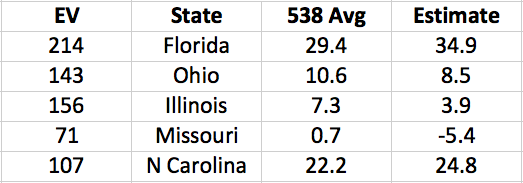
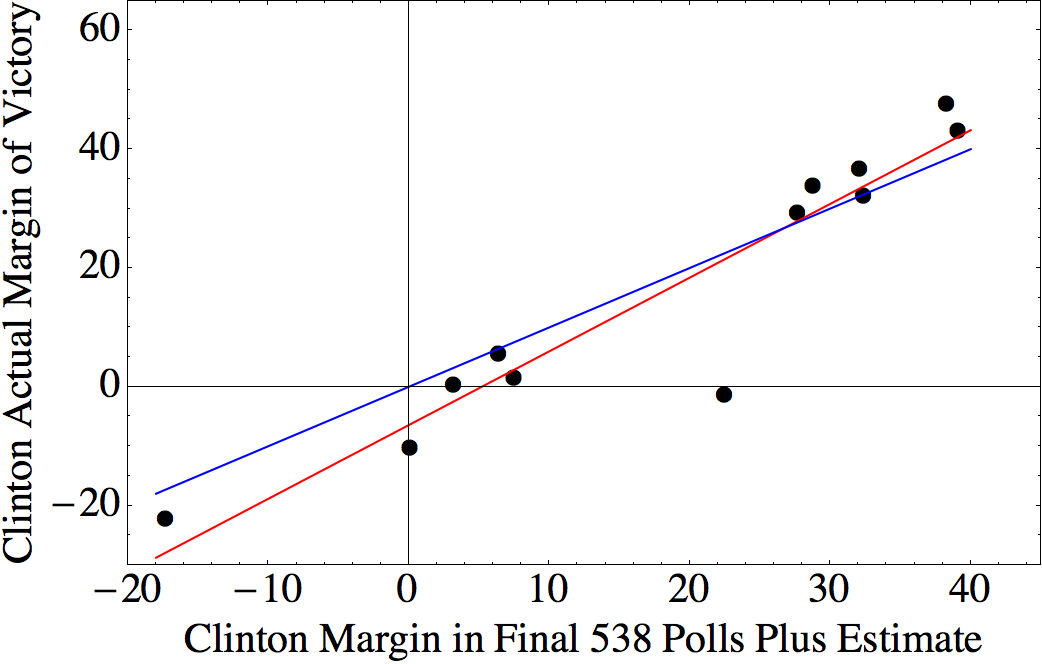
The Cubs wound up the regular season with the best record in baseball: 103 wins (out of only 161 games, due to a rain-out that went down as a tie). Does this guarantee that the Cubs will win it all this year? No. In fact, if you read Slate, “having such a record is nearly a kiss of death.”
Hmm
The premise of the piece seems that winning 100 games actually hurts you in the playoffs, as does having the best regular season record. What follows from that assertion would be an exercise in p-hacking, if any of the supporting evidence were statistically significant. Instead, it is exactly the sort of exercise in anecdotal misinterpretation that statistics were invented to avoid.
It is certainly true that having the best record in the regular season does not guarantee postseason success. Baseball is a game where any team can beat any other on a given day. Typically, only one or two teams win more than 60% of their games over the course of the regular season, and winning 55% will usually get you into the playoffs. When these teams play each other in a best-of-five or best-of-seven series, the odds of the “better” team coming out on top are not much different from a coin toss.
But does it hurt you? Let’s see what stats Slate musters to support the argument. They restrict their analysis to the 21 years from 1995 through 2015, when the playoffs have had the current wildcard structure. During that time:
• No National League team has won 100 regular-season games and won the World Series. The only team in baseball to achieve the feat is the New York Yankees, in 1998 and 2009. Only two 100-win National League teams have even reached the Series.
Okay, during that time period six National League teams and eight American League teams have won at least 100 regular season games. If each playoff was a 50/50 coin toss, each of those teams would have a one in eight chance of winning the world series. So, the expected number of NL wins would be 0.75, and the expected number of AL wins would be 1.0. The NL falls slightly below expectation (0/6), but not significantly so. The AL exceeds expectation (2/8), as does the combined NL-AL record (2/14).
• No team other than the aforementioned 1998 and 2009 Yankees has posted the outright best record in baseball and won the World Series. Boston won the Series in 2007 and 2013 after tying for baseball’s best record.
In five of the 21 years, there was a tie for the best record in baseball. So, in the 16 years with a single best record, that team won the world series twice. Again, coin toss would give you a one in eight chance, so 2/16 is right in line with expectations. In the five years with a tie, there’s a one in four chance that one of those two teams will win, so the expected number of wins would be 1.25, less than the 2/5 Red Sox wins.
• Last year, Kansas City became the seventh team of the wild-card era to post the best record in its league (excluding Boston’s tie in 2007) and win the World Series. In that same span, six wild-card teams have won the Series.
Well, if it’s a coin toss, the team with the best record would have the same odds of winning as the wildcard (or the two wildcards combined, in the extra-expanded playoff structure in place since 2012). So, pretty much what you would expect.
• The top National League team in the regular season hasn’t won the World Series since the Atlanta Braves did it in 1995.
This is the first statistic that seems to deviate at all from expectation. In 21 years, if the top NL team had a one in eight chance of winning the World Series each year, you would expect 21/8 World Series wins. That is, more than two, but fewer than three. And one is less than two, right? Well, the probability that you would have zero wins in 21 years is about 6%. The probability that you would have one win is about 18%.
The standard way to ask this question is to say, “What is the probability that the observed value would deviate by this much or more from expectation”. That probability, in this case, is about 24%. So, not really all that unlikely at all.
Or, in sciencey terms, p=0.24, and we fail to reject the null hypothesis that having the best record in the National League gives you less than a one in eight chance of winning the World Series.
Plus, it’s a bit weird to cherry-pick the top NL team. After all, we were just told that Kansas City was the seventh team to win the World Series after posting the best record in its league. The six cases besides 1995 Atlanta are all from the AL (and exclude the 2007 Red Sox, who tied with Cleveland for the best record).
So what would happen if we asked the analogous AL question. Well, of the 19 years when there was a single top record in the AL, six of those teams went on to win the World Series. The chances of at least six teams doing that, given 1/8 odds, is about 2.5%.
Now, we can’t really read anything into that result, since it is one of a number of statistical tests we did here, so any multiple-tests correction would eliminate the significance of the results. But if we had asked the question about top AL records in isolation, notice that it would have supported the conclusion that having a good regular-season record helps, rather than hurts, your playoff chances.
I wonder why they didn’t include that analysis . . .